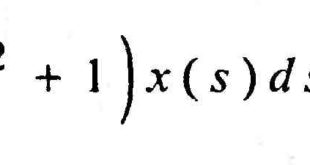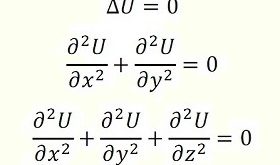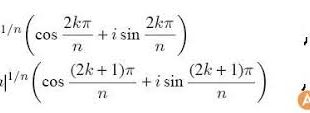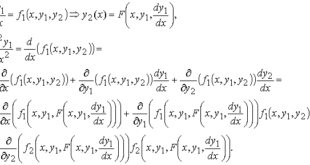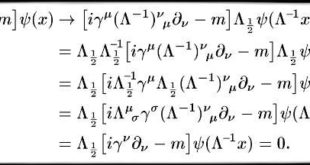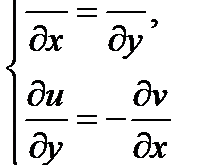علم

موادلة اینتگرالی، معادله‌ای است، که فونکسیة نامعلوم آن تحت علامت اینتگرال واقع است. معادلة اینتگرالی جنس دو­یوم فریدگالم از سادهترین معادلة اینتگرالیست، که در آن 1ر (ج)-فونکسیة نامعلوم، /(ج)-اعضای آزاد، ک (ج، t)-یدرای معادلة اینتگرالی، x-پرمیتر (هم قیمتهای حقیقی و هم قیمتهای کامپلیکسی ق­بول کرده می‌تواند) می‌باشد. در مورد/(ج) “0 …

موادلة لپلس، معادلة دیفرانسیلی حاصله‌هایشان خ و-سوسیی -را گویند: این جا خ# و، گ-تغییریابنده‌های مستقل، ا=u (x، و، خ) فونکسیة مطلوب. این معادله را با­ر اوّل سال 1782 پ. لپلس در اثرهایش عاید به نظریة جاذبه معاینه کرده است. حلّ یک قطار مسئله‌های فیزیکه و تکنیکه با واسطة معادلة لنگرج …

موادلة دوعزای، معادلة نمود ج*-ا=0-را گویند، که در آن ا یگان عدد حقیقی یا کامپلیک­سی می‌باشد. به حل نمودن چنین معادله‌ها مسئلة از ریشة درجة n-م برآوردن عدد ا (ج»= و ا) می‌آورد. معادلة دوعزایی n-تا ریشه‌های گوناگون دارد، که در بین آنها ریشه‌های حقیقی از 2-تا زیاد نیستند. اگر …

موادلة لگرنج، معادی­لة دلمبیر، معادلة دیف­فیرینسیلی عادّی ترتیب یکم را گویند، که نسبت به تغییریابنده‌های وابسته و ناوابسته خطّیست و چنین نمود دارد: ین جا ا’–♦ و/- فونکسیه‌های نسبت به ارگومینتشان دیو-فیرینسیانیدشوندة داده شده. اینتگرال عمومی معادلة لنگرج را در شکل پرمیتری هنگام نسبت به خ دیفّیرینسیانیدن معادله یاف­تن ممکن …

موادلة دیفّیریندسیلی خودپیوست، معادله‌ای است، که با معادلة به خودش همراهشده (پیوسته) هلهای یک‌خِله دارد (نگرید معادله‌های دیفرانسیلی همراهشده). معادلة دیفرانسیلی خودپیوست عادّی ترتیبشان جفت (2m) و ترتیبشان طاق (2ت-1) موافقن شکلهای زیرین را دارند: ک در آن ai فونکسیه‌های خ می‌با­شند. مفهوم معادلة دیفرانسیلی خودپیوست در نظریة معادله‌های دیفرانسیلی …

موادلة کوبی، معادلة الگیبروی ترتیب سوّم نمود اخ9+bx2+سخ-f-d=0-را گویند، که در آن ا^ا می‌با­شد. در این معادله خ-را با نامع­لوم نو او، که با خ توسط برا­بری خ=ا              علاقه‌مند است، یوز    نموده، معادلرا           ب        شکلی نیسبتة ساده       (کنانی)         تبدل          دا­دن ممکن: و3+ر و 4-یه =0. ک در آن و* …

موادلة دیرک، معادلة کونتی حرکت الکترون را گویند، که موافقن به خلاصه‌های نظریة نسبیت مرتّب ساخته توده است (پ. دیرک، سال 1928). از معادلة دیرک برمی‌آید، که الکترون مامینت مقدار  هرکت مکانیکی خاص-سپین. با یاری معادلة دیرک فامولة صحیحتری  سویه‌های انرژیة اتم گید­راگین (و اتمهای هیدروژنمانند) حاصل کرده شد، که …

موادلة کاش-ریمن در نظریة فونکسیه‌های ته-ل ا ل ی، معادلة دیفرانسیلی حاصله‌هایش خصوصی ترتیب یکم را گویند، که وابستگی قسم حقیقی و قسم موهوم فونکسیة تحلیلی w=ا+iv تغییریابنده‌اش کامپلیکسی خ=خ+iy-را افاده می‌کند، یعنی ین نوع معادله‌ها در نظریة فونکسیه‌های تحلیلی و تطبیق آنها به مسئله‌های مکانیکه و فی­زیکه اهمیت کلان …

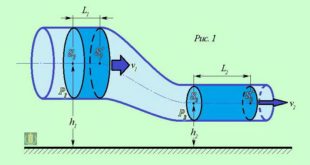
موادلة بیرنولّ در گیدرادینمیکه، معادلة اسا­سی گیدرادینمیکه را گویند، که علاقة بیو سرعت مایع روان (و) و ر فشار آن (ر)-l را هنگام استوار (ستسیانر) بودن جاریشوی افاده می‌کند. دنیال بیرنولّ (1738) از قانون بقای انرژیة مایع واحد حجم استفاده برده این معادله را یافت. در میدان قوّة وزنیوی برای …

موادلة بیرنولّی، در م­تیمتیکه، معادلة دیفّیرین-سیلی ترتیب یکم نمود du -+ر و=qya -را گویند، که این جا ا-عدد ثابته، ر، q-فونکسیه‌های بی‌فاصلة داده شده از خ. با یاری گزارش i- و-ا-م این معادله را به معادلة دیفرانسیلی خطّی نسبت به گ مبدّل کردن ممکن است. این معادله را بار اوّل …