Теги: АЛГЕБРА

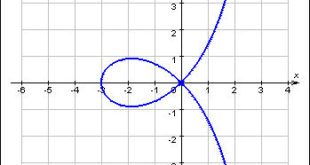
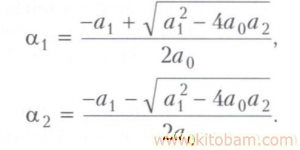ХАТҲОИ ТАРТИБИ ДУЮМ, хатҳои ҳамвореанд, ки координатаҳои росткунҷаи онҳо муодилаи алгебравии дараҷаи дуюмро қонеъ мегардонанд. Масалан, эллипс, (аз ҷумла, давра), гипербола ва парабола аз ҳамин қабиланд.

ТЕОРЕМАИ АСОСИИ АЛГЕБРА, номи теоремаест, ки мавҷудияти решаҳои комплексии муодилаи алгебравии коэффициентҳояш комплексии собит мекунад. Таърифи теорема: ҳар гуна бисёрузваи коэффициентҳояш дилхоҳи дараҷааш калон ё баробари як лоақал як реша (дар ҳолати умумӣ решаи комплексӣ) дорад. Ин теорема яке аз комёбиҳои бузурги тамоми матаматика буда, дар соҳаҳои мухталифи илм истифода …

СТРОФОИДА (аз юнонӣ strophos — лентаи тобхӯрда ва eidos — шакл), хати каҷи алгебравии тартиби сеюмро гӯянд, ки муодилааш дар системаи координатаҳои декартӣ мебошад. Аввалин маротиба Э. Торичелли омӯхтааст (1645).

МУОДИЛАИ АЛГЕБРАВӢ, муоди­лаи намуди /п—0-ро гӯянд, ки дар он /п бисёрузваи дараҷаи n-уми як ё бисёртағйирёбандадор (барои л>0) аст. Муодилаи алгебраи якномаълума на­муди зерин дорад: а0х* в|Хл“* + … + ап = 0,      (1) ин ҷо п — адади бутуни ғайриман­фӣ, «о, А|, …, en — коэффиси­ент ҳ о и …