Назарияи Гаула

Назарияи гаула, назарияи муодилаҳои алгебравии дараҷаашон олии якномаълума, яъне муодилахои намуди

х^п + а₁х ^n–1 + а₂ ^n–2… + а_п-1 x +a_n = 0, (1)

-ро гӯянд, ки онро математики франсавӣ Э. Галуа таҳия кардааст. Масъалаи асосии Н. Г. чунин аст: ҳалли муодилаи (1) бояд бо ёрии чор амали арифметикӣ ва решабарорӣ тавассути коэффисиентҳояш ифода карда шавад. Ҳалли муодилаҳои да­раҷаи 2, 3 ва 4 бо радикалҳо ифода карда мешавад. Ҳалли муодилаҳои дараҷаи 2 аз давраҳои қадим ин ҷониб маълум аст. Ҳалли муодилаи да­раҷаи 3-ро бо ёрии формулоӣ Карда­но ёфтан мумкин аст. Роҳи ҳалли му­одилаи дараҷаи 4-ро математики италиявӣ  Л. Феррарӣ нишон дод. Ма­тематикон барои дар радикалҳо ҳал намудани муодилаи дараҷаи 5-ро 3 аср (асрҳои 16—10) ҷустуҷу карда бошанд ҳам, натиҷае ҳосил карда натавонистанд. Соли 1824  Н. Абел нишон дод, ки муодилаи дараҷаи 5 дар ра­дикалҳо умуман ҳалнопазир мебо­шад. Ҳамин тавр, вақте ки Галуа муодилаҳои алгебравиро тадқиқ менамуд, натиҷаҳои бисёре ба даст омаданд, вале ягон назарияи умумӣ дар бораи муодилаҳои намуди (1) вуҷуд надошт. Macалан, 1) шартҳои зарурӣ ва кофии дар радикалҳо ҳал доштани муодилаи (1); 2) ба кадом намуди силсилаи муодилаҳои нисбатан оддӣ овардани ҳалли муодилаи (1); 3) шартҳои зарурӣ ва кофии ба силсилаи муодилаҳои дараҷаи 2 овардани муодилаи (1) муайян набуданд. Ҳаман ин масъалаҳоро Га­луа дар «Ёддоштҳо доир ба шартҳои ҳалпазирии муодилаҳо дар радикал­ҳо» ном асараш ҳал намуд. Галуа барои ҳалли ин масъалаҳо вобастагии хосиятҳои муодилаҳо ва гурӯҳи гузоришотро тадқиқ намуд ва дар айни ҳол як қатор мафҳумҳои умдаи назарияи гурӯҳҳоро ҷорӣ кард. Ӯ инчунин шартҳои дар радикалҳо ҳал доштани муодилаи (1)-ро тавассути мафҳумҳои назарияи гурӯҳҳо баён намуд. Баъди Галуа ин назария дар бисёр соҳаҳо инкишоф ёфтанд. Ҳозир Назарияи Гаула гуфта назарияеро мефаҳманд, ки ин ё он объектҳои математикиро дар асоси гурӯҳи автоморфизмҳо меомӯзад.

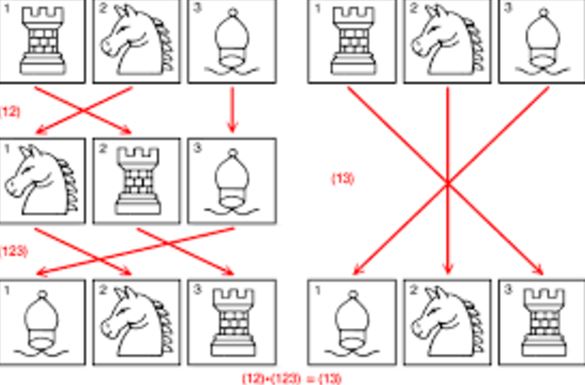
Ад.: Постников М. М., Теория Га­луа, М., 1963.