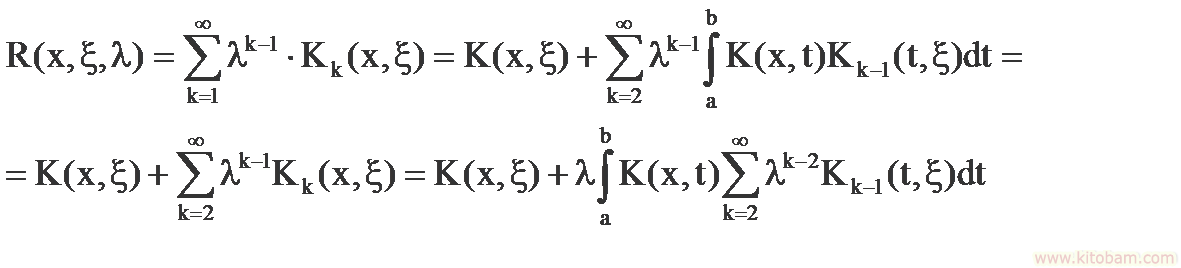
РЕЗОЛВЕНТА

РЕЗОЛВЕНТА (аз лотинӣ гезо1уеп-Из — мифтоқ, гиреҳкушо) дар математика, муодила, функсия (ядро) ё худ оператори мифтоҳиеро гӯянд, ки дар ҳалли муодилаҳои операторӣ истифода мешавад. Дар алгебра истилоҳи «Резолвента» ба чанд маънӣ истифода мешавад. Масалан, Резолвентаи муодилаи алгебравии / (х) = 0-и да-раҷаи п гуфта, чунин муодилаи алгебравии £(х) = 0-ро меноманд, ки коэффисиентҳояш ба коэффисиентҳои 1(х) ратсионалӣ  вобастаанд ва донистани решаҳои он барои ёфтани решаҳои муодилаи ](х) = 0 им-кон медиҳад. Масалан, муодилаи

V3 — ав1>* + (а\а& — 4а4)и — (‘о,,а4 — — 4а2а4 + а%7) = 0

яке аз Р,-ҳои кубии муодилаи дарз-ҷаи чоруми х4 + а,х3 + аз** + озх + 04 = 0     (1)мебошад. Агар ы,, *>2, о$ решаҳои ии Резолвента  бошанд, он гоҳ решаҳои *\, х2, х4-и муодилаи (1) дар натиҷаи ҳал кардани муодилаҳои квадратии а2 — + а4 = 0, к = 1, 2, 3 бароварда мешаванд. Яъне агар г)л решаҳои муодилаҳои квадратӣ бошанд, х,х2 =     *з*4 == т)|. «1*3 = |г, Х2Х4 = Т)2, *\*4 = Ёз,       — Т)3, “= ||^2/т)з ва ғайра мебошад. Дар наза-рияи муодилаҳон интегралӣ РезолвентаР.-и (яд-рои мифтоҳ) муодилаи Ф (•) + *(•, ЩФ Щ = !(•) (2) а гуфта, функсияи Г(з, 1\ Х)-«и аз тағйирёбандаҳои, I ва параметри X вобастаро мефаҳманд, ки тавассути он ҳалли муодилаи (2)-ро дар намуди / (•) + Я. / Р (•, <, X) ((() <И навиштан мумкин. Дар назарияи операторҳои хаттӣ Резолвентаи оператори А оилаи операторҳои = (Л — ХЕ)-1 мебошад, ки дар он параметри комплексии X ҳамаи қиматҳои ба спектри оператори А номутааллиқро қабул карда метавонад.