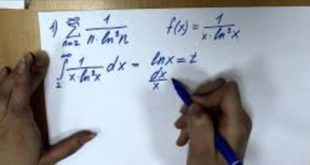Назира (ар. муаннаси мисл, монаид), як шакли анъанавии шеър, ки дар адабиётҳои Шарқи Наздик ва Миёна интишор ёфта буд. Назира сарфи назар аз мавриди гуфта шуданаш ҳамеша як навъ қувваозмоӣ, имтиҳону санҷиши маҳорат ва мусобиқаи адабӣ мебошад. Адиби назирагӯй аксар барои нази расароӣ асарҳои беҳтарин ва машҳуртарини адибони бузурги гузашта …

Назим ( Абдулбоқихоҷаи Бебок (соли таваллуд ва вафоташ номаълум), шоири асри 19 тоҷик. Ҳашмат дар «Тазкират-уш-шуаро» номи ӯро Сайид Муҳаммадхоҷа зикр кардааст. Дар мадрасаҳои Бухоро таҳсил ва баъд мударрисӣ кардааст Аз айёми таҳсил бо тааллуси «Бебок» шеър мегуфтааст, вале дар охири умр «Назим» тахалл. кардааст. Мувофиқи маълумоти тазкираи Возеҳ «Тӯҳфат-ул- …

Наззоми метеорӣ (аз ар.— тезчашм, дурбин, дақиқбин ва метеорҳо) як системаи агрегатҳои фотографист, барои мушоҳидаи метеор (шиҳоб)-ҳо. Ҳар як агрегати Наззоми метеорӣ одатан аз 4—6 камераи фотографии фарохзовия иборат аст. Камераҳоро тавре ҷой медиҳанд, ки онҳо якҳоя қисми ҳаддалимкон калонтарини осмонро дар бар гирифта тавонанд. Macалан, Наззоми метеории Институти астрофизика …

Наззом (тахалл., номаш Иброҳим ибни Сайёр ибни Хонӣ; соли таваллудаш номаълум, Балх — тахм. 845), файласуфи арабзабони форс-тоҷик. Дар Басра таҳсил кардааст. Наззом доир ба масъалаҳои мухталифи фалсафӣ асарҳои зиёде таълиф кардааст, лекин онҳо то имрӯз боқи намондаанд. Афкори фалсафии Наззом дар асарҳои Абумансури Бағдодӣ, Муҳаммади Шаҳристонӣ, Азудуддини Иҷӣ, Насируддини …

Наздикшавӣ, мафҳуми математикиест, ки ҳудуд доштани бузургии тағйирёбандаро ифода мекунад. Ба ҳамин маъно дар бораи Наздикшавии пайдарпаи, Наздикшавии касри бефосила, Наздикшавии зарби беохир, Наздикшавии интеграл ва ғайра сухан рондан мумкин аст. Наздикшавии пайдарпаии {аn} (п = 1, 2, …) ҳудуди охирнок доштани пайдарпай, яъне lim ап = а; Наздикшавии қатори …

Наздикшавии шарти, мафҳу­ми таҳлили математикист. Агар қа­тори наздикшавандаю            қатори n аp қиматҳои мутлақи узвҳои он тар- тиб додашуда  ип| дуршаванда бошанд, қатори n шартан наздик- шаванда номида мешавад. Маcалан, қатори  шартан наздикшаванда мебошад, зеро қатори аз ниматҳои мутлақи узвҳои он тартибдодашуда — (қатори гармоникӣ) дуршаванда аст. Агар қатор шартан наздик- …

Наздикшавии мутлақ дар математика, яке аз навъҳои наздикшавии қаторҳо ва интегралҳост. Агар қатори аз қиматҳои мутлақи ҳар як аъзои қатори u1 + u2 + … + un + … тартиб додашуда |u1|+|u2|+…+|un|+… наpдикшаваyда бошад, қатори ададии u1 + u2 + … + un + …  мутлақ наз­дик шаванда номида мешавад. …

Наздикшавии мунтазам, ҳолати хусусии мафҳуми наздикшавист. Агар барои дилхоҳ  ε > 0 чу­нин N = N(ε) мавҷуд бошад, ки ба­рои он нобаробарии | f(х) —fn(х) | < ε ҳангоми п > N ва барои ҳамаи нуқтаҳои x-и маҷмӯи додашуда иҷро шавад, пайдарпаии функсияҳои fn (x) ( n = 1,  2, …