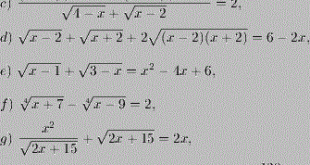Таджикистан – Энциклопедия на таджикском языке КИТОБАМ

МУОДИЛАИ ИРРАСИОНАЛИ, муодилаест, ки дар он бузургии но­маълум дар радикал (реша) мебо­шад, масалан, Уж — 2*5. Барои муоди­лахои иррасионали мафхуми «тартиби муодила» вучуд надорад. Асосан се усули хал кардани муодила­хои иррасионали маъмул аст: 1) усули чори намудани номаълуми ёрирасон, ки баъди он халли Муожилаи иррасионали ба халли муодилаи расионали бадал …

МУОДИЛАИ КЛЕРО, муодилаи дифференсиалии оддии тартиби якуми намуди у — ху’ + /(у#)“РО гир­анд, ки дар он / функсияи диффе- ренсиронидашавандаи додашуда аст. Муодилаи мазкурро бори аввал соли 1734 математики франсави А. Клеро (1713—65) тадкик кардааст. Муодилаи Клеро дар шакли охирнок интегронида ме­шавад. Халли умумии Муодилаи Клеро  план хатхои рости …

МУОДИЛАИ КВАДРАТИ, муоди­лаи намуди ах*+Ьх+с — 0-ро гуянд, ки дар он а, Ь, с ададхои ихтиёри буда, коэффисиентхои муодила но­мида мешаванд. Муодилаи квадрати ду реша до­рад, ки аз руи формулахои ^ _ — Ь +У Ь’—4ас 1          Та 1 b —У bt—iae 2 а хисоб карда мешаванд. Ифодаи D = …

МУОДИЛАХОИ ХАМЧОЯ, системаи муодилахоест, ки барои онхо системам киматхои хамаи муодилахои додашударо конеъгардонанда мавчудаст. Macалан, муодилахои хг + +у2 = 13 ва х 4* у — 5 хамчояанд, зеро киматхои х = 2 ва у – 3 онхоро конеъ мегардонанд; муодиладои х2 4- у2 = 13 ва 2х2 4- 2у2 …

МУОДИЛАИ КЕПЛЕР, муодилаи транссендентиеро гуянд, ки намудаш у — с sin у = х аст. Тадкики Муодилаи Кеплер хангоми |с| < 1 будан басо мухим аст. Ин холат ба мавриде мувофик В меояд, ки у аз руи е ва 1« додашуда танхо як карат муайян карда мешавад. Муодилаи мазкурро бори …