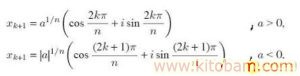МУОДИЛАИ ДУАЪЗОИ

МУОДИЛАИ ДУАЪЗОИ, муодилаи намуди ж* — а = 0-ро гуянд, ки дар он а ягон адади хакики ё комплек­си мебошад. Ба хал намудани чунин муодилахо масъалаи аз решаи дарачаи n-ум баровардани адади а (ж »= у а) меоварад. Муодилаи дуаъзои n-то решахои гуногун дорад, ки дар байни онхо решахои хакики аз 2-то зиёд нестанд. Агар а адади мусбат бошад, яке аз ин решахо — решаи арифме­тики мусбат мебошад. Хангоми ба таври геометри дар хамвории комп­лекси тасвир намудани ададхо хамаи решахои Муодилаи дуаъзои дар даврае вокеъ мегарданд, ки маркази он нуктаи О буда, радиусаш ба решаи арифме­тики аз модули адади а (дар куллахои п-кунчаи мунтазам) баробар мебошад.

Муодилахои дуаъзоии махсуси на­муди X” — 1=0 мухиманд; решахои ин гуна муодилахо решахои дарачаи n-ум аз як номида мешаванд ва шаклашон чунин аст:

2 лк     2 r.k

е* = COS     1- I Sin — ,

п                    п

X — 0, 1, …, п — 1.

Назарияи муодилахои дуаъзои ба­рои ёфтани шартхои масъалаи хеле кадим: бо ёрии паргор ва хаткашак ба кисмхои баробар таксим намудани давра кумак расонд.

Адабиёт: К у р о ш А. Г., Курс высшей ал­гебры, 11 издание, Москва, 1975.